Du rabotage itératif sur les bidulèdres
Le procédé est assez simple : au rang 0 vous partez d'un polyèdre quelconque, par exemple un tétraèdre régulier.
n = 0
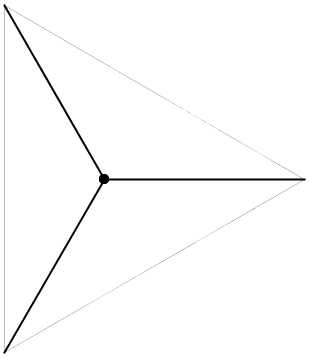
Pour obtenir les sommets du bidulèdre de rang 1, vous prenez le milieu de chaque arête du rang 0.
n = 0
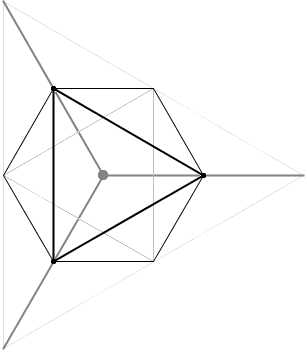 n = 1
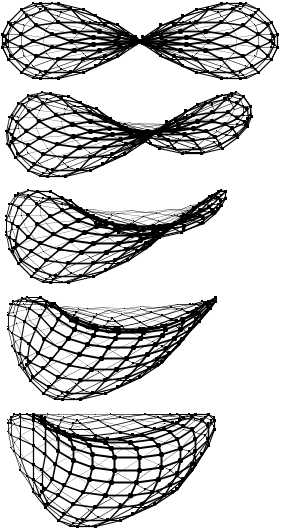
n = 1Et vous recommencez, jusqu'au moment où vous en avez marre.
n = 1
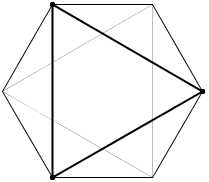
n = 2
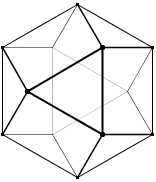
n = 3
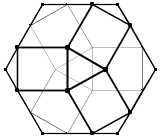
n = 4
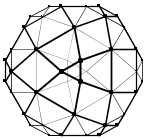
n = 5
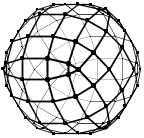
n = 6

n = 7
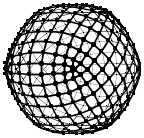
Je me pose la question suivante : vers quelle surface converge-t-on ?
Par exemple dans le cas où n = 0 est un tétraèdre régulier, converge-t-on vers la sphère inscrite ? Bof... ce serait étonnant en fait.
Une surface tangente en leur centre à chacune des faces du bidulèdre initial, certes, mais laquelle ?
Voici ma conjecture : la suite converge vers un bidulèdre.
Et dans le cas où n = 0 est un bidulèdre concave...
n = 0
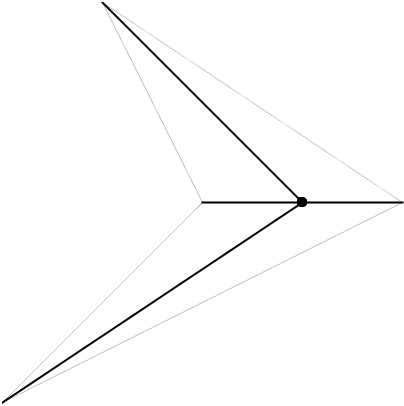
n = 5
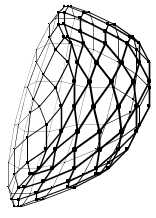
n = 7

... on obtient une pastille contre la toux.
Etonnant, non ?
Et si on place les 5 points du bidulèdre initial différemment, on obtient ce truc :
n = 6
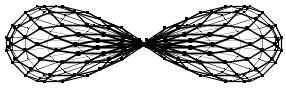
On peut donc passer du premier au deuxième bidulèdre continûment.
Remarquons sur ce dernier exemple qu'il serait peut-être souhaitable de "rafiner" le bidulèdre d'autant plus que la courbure locale est grande.
Les sommets des bidulèdres de rang n + 1 sont générés en prenant les milieux des segments du bidulèdre de rang n.
Donc les sommets d'un bidulèdre quelconque sont des barycentres à coefficients entiers des sommets du rang 0 .
Le gros du travail, en partant d'un tétraèdre par exemple, consiste à calculer les quadruplets d'entiers pondérant chaque sommet.
Le positionnement des sommets dans l'espace et le rendu sont ensuite très rapides.
On pourrait imaginer une évolution de l'application permettant de déplacer les sommets de départ et de visualiser immédiatement l'impact sur le bidulèdre de rang final, sans recalculer les pondérations.
Mais bon, pas le temps, pas le courage.
Pour finir, une question de topologie, à mon avis imbitable :
combien de sommets au minimum faudrait-il au bidulèdre de rang 0 pour représenter le retournement de la sphère ?
Est-ce qu'on s'en sortirait avec 5 ?
Deux possibilités :
ou 5 est insuffisant, et ça m'étonnerait un petit peu,
ou 5 est suffisant, et ça m'étonnerait beaucoup.
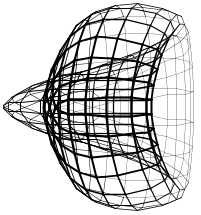
Et tout cas, avec 7, on arrive à imiter le début...