Babel

La confusion des langues, Gustave Doré
Salut à toi, Gloumouth3,
avec qui j'ai partagé
quelques années durant
un intérêt (probablement un peu excessif)
pour les ordinateurs.
On était en classe de première,
je dirais vers la fin d'année.
L'été approchait,
et rien d'intéressant ne se passait.
Vraiment rien.
Quand soudain,
on s'est dit
"tiens, et si on codait un moteur de rendu 3D ?!"
En tatonnant, certes,
maladroitement, peut-être,
poussivement, même,
on a pondu notre truc.
Et d'une certaines manière,
je crois qu'on s'est bien marré.
J'ai perdu le code source depuis longtemps.
Il doit croupir sagement sur une disquette,
probablement dans une décharge.
Mais subsistent quelques impressions papier,
sur lesquelles je suis retombé.
Celle-ci par exemple :
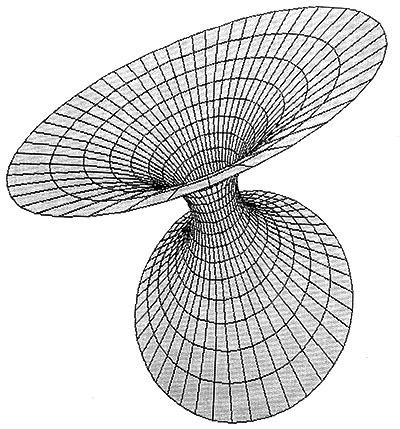
En noir et blanc, la définition était presque correcte,
mais dès qu'on voulait se permettre le luxe
d'avoir la couleur,
c'était franchement pas terrible.
Ne me demandez pas pourquoi,
j'ai oublié.

Ces images ont presque une valeur sentimentale à mes yeux.
Pour la petite histoire, vous pouvez les visualiser
grâce à ce que j'appelerais
une "hérésie numérique" absolue.
Etant donné qu'on ne sauvegardait pas nos images,
la chaîne rocambolesque aboutissant à vos mirettes
est à peu près la suivante :
| 1) | vers 1993, on a généré ces images |
| 2) | on a pris l'écran à tube cathodique en photo (avec un appareil argentique, bien sûr) |
| 3) | on a fait développer tout ça sur papier 10x15 |
| 4) | on a trouvé que c'était pas assez grand, alors on les a agrandies grâce à une photocopieuse couleur |
| 5) | j'ai perdu ces photos et leurs agrandissements |
| 6) | 20 ans se sont passés |
| 7) | j'ai retrouvé les agrandissements il y a quelques jours, et les ai pris en photo (numérique cette fois) |
| 8) | et par la grâce d'Internet, ils sont maintenant devant votre nez |
Franchement,
ces photocopies de photos d'écran,
était-ce bien sérieux ?

Nous avions absolument tout fait "à la main"
et réinventé la roue dans ses moindres détails.
La roue était un peu voilée sur les bords,
mais c'était assez héroïque quand j'y réfléchis.
Nous n'avions pas conscience
qu'il était possible de se procurer
une littérature spécialisée
et Internet n'existait pas encore,
du moins pour le grand public.
On était donc coupé de tout, ou presque,
et nous avions codé patiemment
toutes les "primitives graphiques" nécessaires.
Jusqu'à l'algorithme de remplissage des triangles,
pixel par pixel.
Tout, absolument tout,
Les calculs matriciels,
Les faces cachées,
les produits vectoriels
pour l'illumination en chaque point.
Ca nous a occupé presque
la totalité de notre temps libre
pendant plus de six mois.
J'avais fini par m'attacher
à cet outil inutilisable par d'autres que nous,
et peut-être plus ou moins consciemment
inspiré par Doré ou Bruhegel,
j'avais eu l'idée de représenter
une Tour de Babel stylisée.

Et maintenant,
20 ans après,
ladies and gentlemen,
calculé en direct live dans votre navigateur,
voici ce qui m'a demandé moins de 100 lignes de code :
et beaucoup, beaucoup moins de temps :
Je vous conseille de changer de navigateur
(ou carrément de bécane)
pour que l'animation ci-dessus s'affiche correctement !
Si vous voulez manipuler l'objet,(ou carrément de bécane)
pour que l'animation ci-dessus s'affiche correctement !
cliquez ici.
Je mesure le chemin parcouru,
l'effort accompli dans le domaine,
pour définir certaines normes, API, libraries,
pour abstraire l'accès aux ressources matérielles...
En somme,
pour réduire la Confusion des langues.
Cela dit, avec le recul, aujourd'hui,
je me demande si ma Tour de Babel
ne m'évoque pas plus
une glace à la chantilly,
ou un étron de Schtroumpf sous acide.
De plus, pour être honnête,
on reste quand même assez loin
de ce ce que permettent certains moteurs de rendu :

Mouais...
Pas sûr que Pixar m'embauche demain.